2020/09/20 - [분류 전체보기] - 분류모형 1.평가척도
#ROC커브 (Receiver Operating Characteristic Curve)
-가로축을 1-특이도 (False Positive Rate) : 0인 케이스에 대해서 1로 잘못 예측한 비율
세로축을 민감도(True Positive Rate) : 1인 케이스에 대한 1로 잘 예측한 비율
로 두어, 시각화한 그래프이다.
-2진 분류(binary classfication)에서 모형의 선능을 평가하기 위해 많이 사용된다.
-그래프가 왼쪽 상단에 그려질수록 올바르게 예측한 비율은 높고, 잘못 예측한 비율은 낮음을 의미한다.
-ROC곡선 아래의 면적을 의미하는 AUROC(Area Under ROC)값이 크면 클수록(1에 가까울수록) 모형의 성능이 좋다고 평가한다.
*ROC커브 이해하기 예제
종속변수의 (Y/N)여부를 이미 알고 있는 모형에 대해 2진분류 모델링을 돌려본 결과 다음과 같은 확률이 나왔다.
| 행번호 | 확률 | 실제 값 |
| 1 | 0.937 | Y |
| 2 | 0.830 | Y |
| 3 | 0.738 | N |
| 4 | 0.720 | N |
| 5 | 0.603 | Y |
이 모형에서 , 확률 값 중 어느정도가 되었을 때 Y로 볼 것인지를 결정해야하는데
예를들어 기준값을 0.936 과 0.829로 했을 때를 생각해본다.
| 행번호 | 확률 | 실제 값 | 0.936기준 | True Posive Rate(민감도) | False Positive Rate(1-특이도) |
| 1 | 0.937 | Y | Y | 1/3 | 0 |
| 2 | 0.830 | Y | N | ||
| 3 | 0.738 | N | N | ||
| 4 | 0.720 | N | N | ||
| 5 | 0.603 | Y | N |
| 행번호 | 확률 | 실제 값 | 0.829기준 | True Posive Rate(민감도) :실제Y중에 맞게 예측한 비율 |
False Positive Rate(1-특이도) :실제 N 중에 틀리게 예측한 비율 |
| 1 | 0.937 | Y | Y | 2/3 | 0 |
| 2 | 0.830 | Y | Y | ||
| 3 | 0.738 | N | N | ||
| 4 | 0.720 | N | N | ||
| 5 | 0.603 | Y | N |
이런식으로 기준을 바꿔가며 계산해보면 다음과같은 표를 얻는다.
| 기준값 | True Posive Rate(민감도) | False Positive Rate(1-특이도) |
| 0.937 | 1/3 | 0 |
| 0.830 | 2/3 | 0 |
| 0.738 | 2/3 | 1/2 |
| 0.720 | 2/3 | 2/2 |
| 0.603 | 3/3 | 2/2 |
이를 표로 그리면 다음과같다.
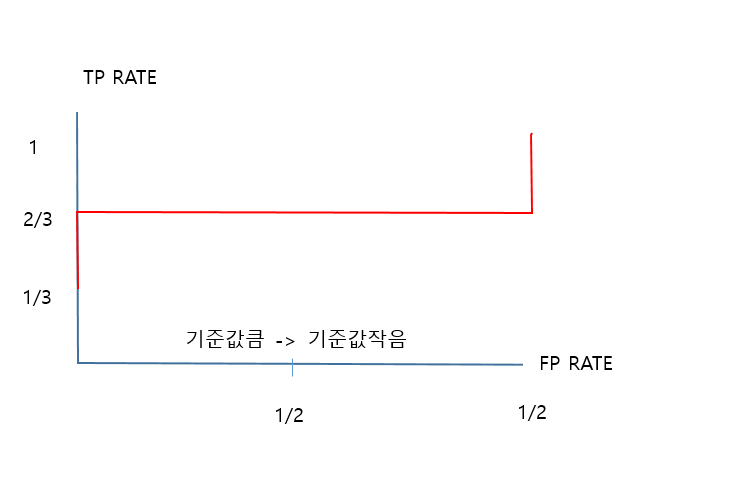
이상적인 ROC 커브는 다음과 같다.
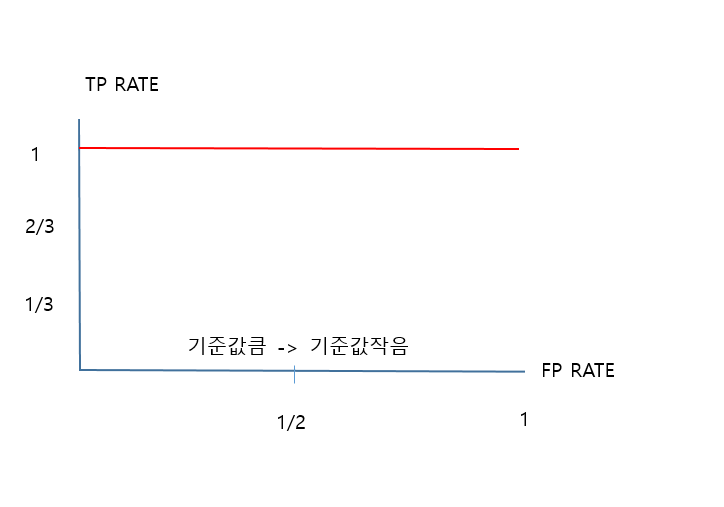
*높은 기준값에도 TP가 높다면 좋은 모델이다.
컷트라인이 높은데도 불구하고 많은 행이 실제로 TRUE고 모델도 TRUE로 예측했기 떄문이다.
*일반적으로 높은 기준값에는 FP(오분류율) 이 적다가 낮은 기준값에서는 FP(오분류율)이 높아진다.
*ROC커브 아래의 면적 AUROC = (Accuracy Ratio+1)/2
아래의 블로그에서 추가적인 설명을 볼수있음
'R프로그래밍,통계학' 카테고리의 다른 글
| 연관분석 - 개념과 R코드로 가시화 하기 (0) | 2020.10.01 |
|---|---|
| 분류모형2-2 분류모형의 평가- 리프트도표/Gain chart (0) | 2020.09.22 |
| 분류모형 1.평가척도 (0) | 2020.09.20 |
| 텍스트 처리 함수 1-1)기본함수 기초(in R) (0) | 2020.09.14 |
| 비정형 데이터분석_정규표현식(in R) (0) | 2020.09.13 |



